この節はイデアルの話題の続きである.
前の節で議論した, GCD を計算するアルゴリズムを
用いると, 1 変数の多項式環の場合, 多項式 ![]() が イデアル
が イデアル ![]() に入っているかどうかを, 計算機を用いて確かめることが可能である.
イデアル
に入っているかどうかを, 計算機を用いて確かめることが可能である.
イデアル ![]() が, 多項式
が, 多項式 ![]() と
と ![]() で生成されているとしよう.
このとき
で生成されているとしよう.
このとき ![]() を
を ![]() と
と ![]() の GCD とすると,
の GCD とすると,
![]() がイデアル
がイデアル ![]() に入っているための必要十分条件は,
に入っているための必要十分条件は,
![]() が
が ![]() を戻すことである.
つまり,
を戻すことである.
つまり, ![]() が
が ![]() で割り切れればよい.
これは
で割り切れればよい.
これは
![]() であることから明らかであろう.
まとめると,
であることから明らかであろう.
まとめると,
2 変数以上のイデアルは, 単項生成とは限らない.
たとえば,
このアルゴリズムは多変数多項式に一般化できる. この一般化されたアルゴリズムの中心部分が Buchberger アルゴリズムである. Buchberger アルゴリズムは, イデアルに入っているかどうかの判定だけでなく, 代数方程式系を解いたり, 環論や代数幾何や多面体や微分方程式論などにでてくる さまざまな数学的対象物を構成するための基礎となっている 重要なアルゴリズムである.
この節では Buchberger アルゴリズム自体の解説は 優れた入門書がたくさんあるので (たとえば [2], [3] など), それらを参照してもらうことにして, Buchberger アルゴリズムの中で重要な役割をはたす割算アルゴリズム (または reduction アルゴリズム) について計算代数システムの内部構造の立場からくわしく考察する. それから Buchberger アルゴリズムと グレブナ基底を簡潔に解説して, イデアルメンバシップアルゴリズムを説明する. 最後にグレブナ基底の別の応用である連立方程式の 求解について簡単にふれる.
イデアルメンバシップアルゴリズムを多変数へ 拡張するには 1 変数の場合と同様にまず initial term を計算する関数を用意しないといけない.
注意すべきは,
2変数以上の場合, さまざまな順序を考えることが可能となることである.
以下 ![]() 変数多項式環
変数多項式環
![]() で議論する.
たとえば
で議論する.
たとえば
![]() なる辞書式順序 (lexicographic order)
は次のように定義する.
なる辞書式順序 (lexicographic order)
は次のように定義する.
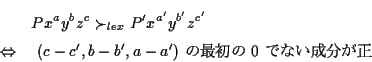
別の順序を考えることも可能である.
たとえば,
![]() を
を ![]() であるような
ベクトルとして,
であるような
ベクトルとして,
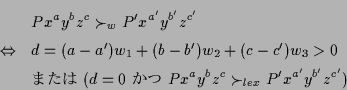
あたえられた順序 ![]() (
(![]() は
は ![]() か
か ![]() )
と多項式
)
と多項式 ![]() に対して,
多項式
に対して,
多項式 ![]() の中の一番大きいモノミアル(単項式)をその多項式の
initial term といい
の中の一番大きいモノミアル(単項式)をその多項式の
initial term といい
![]() と書く.
と書く.
次の関数 in(F) および in2(F) はそれぞれ,
![]() および
および
![]() なる
辞書式順序 (lexicographic order)
で initial term をとりだす関数である.
なる
辞書式順序 (lexicographic order)
で initial term をとりだす関数である.
def in(F) {
D = deg(F,z);
F = coef(F,D,z);
T = z^D;
D = deg(F,y);
F = coef(F,D,y);
T = T*y^D;
D = deg(F,x);
F = coef(F,D,x);
T = T*x^D;
return [F*T,F,T];
}
|
def in2(F) {
D = deg(F,x);
F = coef(F,D,x);
T = x^D;
D = deg(F,y);
F = coef(F,D,y);
T = T*y^D;
D = deg(F,z);
F = coef(F,D,z);
T = T*z^D;
return [F*T,F,T];
}
|