下のプログラムの
encrypt(M) は文字列 ![]() を RSA 暗号化する.
decrypt(C) は encrypt された結果を元の
文字列に戻す.
例を示そう.
を RSA 暗号化する.
decrypt(C) は encrypt された結果を元の
文字列に戻す.
例を示そう.
[356] encrypt("OpenXM");
Block_size = 2
The input message = OpenXM
20336
25966
22605
0
[4113338,3276482,4062967,0]
[357] decrypt(@@);
Block_size = 2
The input message to decrypt
= [4113338,3276482,4062967,0]
20336
25966
22605
0
[OpenXM,[79,112,101,110,88,77]]
|
以下の変数への値の設定プログラムと関数を集めたファイルが rsa.rr である.
PP=1231$
QQ=4567$
EE=65537$
DD=3988493$
/*
PP = 1231, QQ=4567, N=PP*QQ, N'=(PP-1)*(QQ-1)
EE = 65537, (gcd(EE, N') = 1),
DD = 3988493, ( DD*EE = 1 mod N').
(These values are taken from the exposition on RSA at
http://www8.big.or.jp/%7E000/CyberSyndrome/rsa/index.html)
(EE,N) is the public key.
DD is the private key. PP, QQ, N' should be confidential
*/
def naive_encode(S,P,N) {
/* returns S^P mod N */
R = 1;
for (I=0; I<P; I++) {
R = (R*S) % N;
}
return(R);
}
def encode(X,A,N) {
R = 1; P = X;
while (A != 0) {
if (A % 2) {
R = R*P % N;
}
P = P*P % N;
A = idiv(A,2);
}
return(R);
}
def encrypt(M) {
extern EE,PP,QQ;
E = EE; N= PP*QQ;
Block_size = deval(log(N))/deval(log(256));
Block_size = pari(floor,Block_size);
print("Block_size = ",0); print(Block_size);
print("The input message = ",0); print(M);
M = strtoascii(M);
L = length(M);
/* Padding by 0 */
M = append(M,
vtol(newvect((idiv(L,Block_size)+1)*Block_size-L)));
L = length(M);
C = [ ]; S=0;
for (I=1; I<=L; I++) {
S = S*256+M[I-1];
if (I % Block_size == 0) {
print(S);
S = encode(S,E,N);
C = append(C,[S]);
S = 0;
}
}
print(" ");
return(C);
}
def decrypt(M) {
extern DD, PP, QQ;
D = DD; N = PP*QQ;
Block_size = deval(log(N))/deval(log(256));
Block_size = pari(floor,Block_size);
print("Block_size = ",0); print(Block_size);
print("The input message to decrypt = ",0); print(M);
L = length(M);
C = [ ];
for (I=0; I<L; I++) {
S = encode(M[I],D,N);
print(S);
C1 = [ ];
for (J=0; J<Block_size; J++) {
S0 = S % 256;
S = idiv(S,256);
if (S0 != 0) {
C1 = append(C1,[S0]);
}
}
C = append(C,reverse(C1));
}
print(" ");
return([asciitostr(C),C]);
}
end$
encode(X,A,N) は,
![]() を計算する関数である.
native_encode(X,A,N) は
定義どおりにこの計算をする関数である.
この関数をためしてみればわかるように,
工夫してこの計算をしないと大変な時間がかかる.
A を2進展開して計算しているのが, encode(X,A,N)
である.
実行時間を比べてみてほしい.
を計算する関数である.
native_encode(X,A,N) は
定義どおりにこの計算をする関数である.
この関数をためしてみればわかるように,
工夫してこの計算をしないと大変な時間がかかる.
A を2進展開して計算しているのが, encode(X,A,N)
である.
実行時間を比べてみてほしい.
A を2進展開し
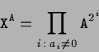
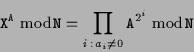
encrypt では,
あたえらた文字列をまずアスキーコードに変換して,
変数 M にいれている.
Block_size を ![]() とするとき,
まず,
とするとき,
まず,
decrypt は encrypt とほぼ同様の操作なので 説明を省略する.
さて次の問題として, RSA 暗号化システムのための
公開鍵 ![]() および秘密鍵
および秘密鍵 ![]() を生成する問題がある.
次のプログラム
rsa-keygen.rr
は, これらの数を生成し, 変数 EE, DD
などに設定する.
を生成する問題がある.
次のプログラム
rsa-keygen.rr
は, これらの数を生成し, 変数 EE, DD
などに設定する.
def rsa_keygen(Seed) {
extern PP,QQ,EE,DD;
random(Seed);
do {
P = pari(nextprime,Seed);
Seed = Seed+P;
Q = pari(nextprime,Seed);
PP = P;
QQ = Q;
Phi = (P-1)*(Q-1);
E = 65537;
Seed = Seed+(random()*Q % Seed);
} while (igcd(E,Phi) != 1);
EE = E;
DD =inv(EE,Phi);
print("Your public key (E,N) is ",0); print([EE,PP*QQ]);
print("Your private key D is ",0); print(DD);
return([PP,QQ,EE,DD]);
}
end$
次の例は,
![]() 程度の
大きさの素数を
程度の
大きさの素数を ![]() 個生成して, RSA の公開鍵, 秘密鍵 を作る例である.
なお, この程度の大きさの素数の積は最新の理論とシステムを用いると容易
に因数分解可能である.
個生成して, RSA の公開鍵, 秘密鍵 を作る例である.
なお, この程度の大きさの素数の積は最新の理論とシステムを用いると容易
に因数分解可能である.
[355] load("rsa.rr")$
[356] load("rsa-keygen.rr")$
[359] rsa_keygen(2^128);
Your public key (E,N) is [65537,
231584178474632390847141970017375815766769948276287236111932473531249232711409]
Your private key D is
199618869130574460096524055544983401871048910913019363885753831841685099272061
[340282366920938463463374607431768211507,
680564733841876926926749214863536422987,
65537,
199618869130574460096524055544983401871048910913019363885753831841685099272061]
[360] encrypt("Risa/Asir");
Block_size = 32
The input message = Risa/Asir
37275968846550884446911143691807691583636835905440208377035441136500935229440
[146634940900113296504342777649966848592634201106623057430078652022991264082696]
[361] decrypt(@@);
Block_size = 32
The input message to decrypt =
[146634940900113296504342777649966848592634201106623057430078652022991264082696]
37275968846550884446911143691807691583636835905440208377035441136500935229440
[Risa/Asir,[82,105,115,97,47,65,115,105,114]]
高速に安全な公開鍵 ![]() および秘密鍵
および秘密鍵 ![]() を生成する問題は,
RSA 暗号ファミリを利用するうえでの一つの中心的問題である.
たとえば,
を生成する問題は,
RSA 暗号ファミリを利用するうえでの一つの中心的問題である.
たとえば, ![]() ,
, ![]() が小さい素数の積に分解する場合は,
比較的高速な
が小さい素数の積に分解する場合は,
比較的高速な ![]() の素因数分解法が知られている.
つまりこのような
の素因数分解法が知られている.
つまりこのような ![]() から生成した
鍵はこの素因数分解法の攻撃に対して脆弱である.
上の関数 rsa_keygen はこのような攻撃に対する脆弱性がないかの
チェックをしていない.
その他, さまざまな攻撃法に対する, 脆弱性がないかのチェックが必要となる.
から生成した
鍵はこの素因数分解法の攻撃に対して脆弱である.
上の関数 rsa_keygen はこのような攻撃に対する脆弱性がないかの
チェックをしていない.
その他, さまざまな攻撃法に対する, 脆弱性がないかのチェックが必要となる.
Risa/Asir は, 楕円曲線の定義する可換群をもちいる暗号系である, 楕円暗号系に関して, 安全なこれらのパラメータを生成する システムの基礎部分として実際に利用されている. Risa/Asir に組み込まれている, 大標数有限体の計算機能および 高速な 1 変数多項式の計算機能はこれらに必要な機能として開発された.