Next: Competitive distributed computation by Up: Distributed computation with homogeneous Previous: Distributed computation with homogeneous
Shoup [18] showed that the product of univariate polynomials with large degrees and large coefficients can be computed efficiently by FFT over small finite fields and Chinese remainder theorem. It can be easily parallelized:
Input :such that
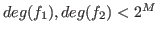
Output :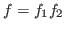
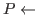
where
is an odd prime,
and
is sufficiently large.
Separateinto disjoint subsets
.
forto
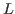
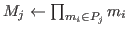
Computesuch that
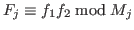
andin parallel.
(The product is computed by FFT.)
return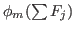
(For,
and
)
Figure 3
shows the speedup factor under the above distributed computation
on Risa/Asir. For each ![]() , two polynomials of degree
, two polynomials of degree ![]() with 3000bit coefficients are generated and the product is computed.
The machine is FUJITSU AP3000,
a cluster of Sun workstations connected with a high speed network
and MPI over the network is used to implement OpenXM.
with 3000bit coefficients are generated and the product is computed.
The machine is FUJITSU AP3000,
a cluster of Sun workstations connected with a high speed network
and MPI over the network is used to implement OpenXM.
If the number of servers is ![]() and the inputs are fixed, then the cost to
compute
and the inputs are fixed, then the cost to
compute ![]() in parallel is
in parallel is ![]() , whereas the cost
to send and receive polynomials is
, whereas the cost
to send and receive polynomials is ![]() if ox_push_cmo() and
ox_pop_cmo() are repeatedly applied on the client.
Therefore the speedup is limited and the upper bound of
the speedup factor depends on the ratio of
the computational cost and the communication cost for each unit operation.
Figure 3 shows that
the speedup is satisfactory if the degree is large and
if ox_push_cmo() and
ox_pop_cmo() are repeatedly applied on the client.
Therefore the speedup is limited and the upper bound of
the speedup factor depends on the ratio of
the computational cost and the communication cost for each unit operation.
Figure 3 shows that
the speedup is satisfactory if the degree is large and ![]() is not large, say, up to 10 under the above environment.
If OpenXM provides collective operations for broadcast and reduction
such as MPI_Bcast and MPI_Reduce respectively, the cost of
sending
is not large, say, up to 10 under the above environment.
If OpenXM provides collective operations for broadcast and reduction
such as MPI_Bcast and MPI_Reduce respectively, the cost of
sending ![]() ,
, ![]() and gathering
and gathering ![]() may be reduced to
may be reduced to ![]() and we can expect better results in such a case. In order to implement
such operations we need new specifications for inter-sever communication
and the session management, which will be proposed as OpenXM-RFC 102.
We note that preliminary experiments show the collective operations
work well on OpenXM.
and we can expect better results in such a case. In order to implement
such operations we need new specifications for inter-sever communication
and the session management, which will be proposed as OpenXM-RFC 102.
We note that preliminary experiments show the collective operations
work well on OpenXM.
Nobuki Takayama 2017-03-30