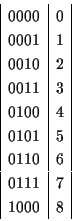
計算機の扱える情報は 2 進数である. それらにたいする, 四則演算と記憶ですべての処理が すすむ. これを常に念頭において勉強していくのが, 理解の早道であろう.
2進数で 8 桁の情報を 1 byte とよぶ.
メモリは各番地に 1 byte の情報を格納できる.
2進数は 0 と 1 の 2 つの記号を用いて数を表現する.
2進数と 10進数の対応は以下のとおり.
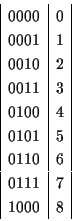
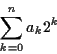
2 進数を書くのは桁が多くて面倒なので, 代わりに 普通 16 進数を使うことが多い. 16 進数 2 桁が 2 進数 8 桁に対応するので換算が簡単である. 16 進数では

|

|
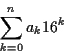
計算機が数を有限桁の 2 進数で表現していることを 実感する例として次の計算をやってみるのはおもしろいであろう. コマンド pari(sqrt,n) を用いると, n の平方根を指定した精度で計算できる. 詳しくは, 索引およびマニュアルの eval および setprec を見よ.
[346] 2+pari(sqrt,3); 3.73205080756887729346530507834 [347] 1/(2-pari(sqrt,3)); 3.73205080756887729266193019921
![]() の分母を有理化すると
の分母を有理化すると
![]() に等しいはずだが, 近似的な数値計算では
このように誤差が生じる.
に等しいはずだが, 近似的な数値計算では
このように誤差が生じる.
Asir では教育用にメモリーを直接覗いたり操作したりする, peek と poke という関数がついている. これらの関数を用いるとメモリに数が格納されている様子を観察 できる. これらの関数については 第 11 章を見よ.