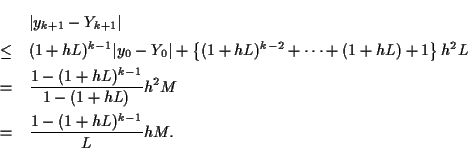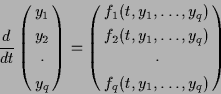: 例
: 常微分方程式の数値解
: 不安定現象
目次
索引
定理の意味を説明しよう.
 は
は  に依存しないので,
式 (9.3) の右辺は,
に依存しないので,
式 (9.3) の右辺は,
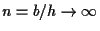 のとき
のとき 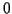 に収束する.
したがって,
に収束する.
したがって,  が十分大きいとき
(すなわち
が十分大きいとき
(すなわち  が十分小さいとき),
差分法で求まる数列
が十分小さいとき),
差分法で求まる数列 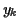 は真の解
は真の解 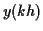 に
に
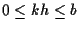 の区間で十分近い.
の区間で十分近い.
定理の証明をしよう.
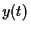 を真の解とし,
を真の解とし,
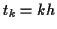 ,
, 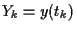 とおく.
とおく.
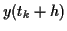 に Taylor 展開の公式を
に Taylor 展開の公式を 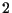 次まで適用すると,
等式
次まで適用すると,
等式
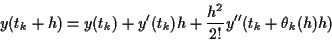 |
(9.4) |
が成立する.
ここで, 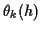 は
は 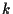 と
と 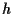 に依存し,
に依存し,
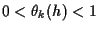 を満たす定数である.
(9.4) を微分方程式を用いてかきなおすと,
を満たす定数である.
(9.4) を微分方程式を用いてかきなおすと,
となる.
差分方程式の方の解 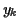 と差をとると,
と差をとると,
を得る.
よって不等式
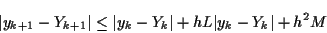 |
(9.5) |
を得る.
ここで 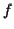 のリプシッツ連続性および,
区間
のリプシッツ連続性および,
区間 ![$[0,b]$](img354.png) で
で 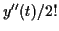 が有界であり, ある定数
が有界であり, ある定数 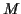 で上からおさえられることを用いた.
(9.5) の右辺の
で上からおさえられることを用いた.
(9.5) の右辺の 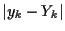 を
を
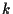 ,
, 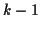 に対する場合の不等式 (9.5) で上から
おさえることにより,
に対する場合の不等式 (9.5) で上から
おさえることにより,
をえる.
これを繰り返して,
ここで
なので,
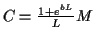 とおくと, 定理の不等式がみたされる.
証明おわり.
とおくと, 定理の不等式がみたされる.
証明おわり.
同様の差分化および証明法は連立常微分方程式
でも通用する.





: 例
: 常微分方程式の数値解
: 不安定現象
目次
索引
Nobuki Takayama
平成15年9月12日
![]() は
は ![]() に依存しないので,
式 (9.3) の右辺は,
に依存しないので,
式 (9.3) の右辺は,
![]() のとき
のとき ![]() に収束する.
したがって,
に収束する.
したがって, ![]() が十分大きいとき
(すなわち
が十分大きいとき
(すなわち ![]() が十分小さいとき),
差分法で求まる数列
が十分小さいとき),
差分法で求まる数列 ![]() は真の解
は真の解 ![]() に
に
![]() の区間で十分近い.
の区間で十分近い.
![]() を真の解とし,
を真の解とし,
![]() ,
, ![]() とおく.
とおく.
![]() に Taylor 展開の公式を
に Taylor 展開の公式を ![]() 次まで適用すると,
等式
次まで適用すると,
等式