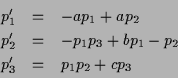: 数の内部表現
: 常微分方程式の数値解
: 解の収束定理
目次
索引
以下は常微分方程式を数値的に解く例である.
どのような差分スキームをもちいているか,
プログラムを読んで述べよ.
例題 9.2
を数値的に解く.
load("glib")$
def diff1(X1,X2) {
glib_open();
glib_window(-10,-10,10,10);
glib_line(-10,0,10,0);
glib_line(0,-10,0,10);
Dt=deval(0.001); T=deval(0.0);
while (T < 10) {
Y1=X1+Dt*X2;
Y2=X2-Dt*X1;
glib_putpixel(X1,X2);
T=T+Dt;
X1=Y1; X2=Y2;
}
}
print("Type in, for example, diff1(2,3); ")$
end$
例題 9.3
を数値的に解く.
load("glib")$
def diff2(X1,X2) {
glib_open();
glib_window(-10,-10,10,10);
glib_line(-10,0,10,0);
glib_line(0,-10,0,10);
Dt=deval(0.001); T=deval(0.0);
while (T < 50) {
Y1=X1+Dt*X2;
Y2=X2+Dt*(-X1-0.1*X2);
glib_putpixel(X1,X2);
T=T+Dt;
X1=Y1; X2=Y2;
}
}
print("Type in, for example, diff2(2,3); ")$
end$
例題 9.4 強制振動の方程式
を数値的に解いてみよう.
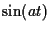
が外部から単振動する物体に与えられる力である.
この例題は,
5 章においてすでに紹介した.
このように, 微分方程式を数値的に解く事を数値解法という.
この方法は, ゲームから, LSI の設計, 飛行機の設計までさまざまな
場面で利用されている.
最後は カオス的力学系の例である.
例題 9.5
Lorentz 方程式
の解を眺めてみよう.
ここで
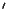
は
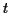
についての微分をあらわす.
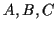
はパラメータである.
load("glib")$
def lorentz() {
glib_window(-25,-25,25,25);
A=10; B=20; C=2.66;
P1=0; P2 = 3; P3 = 0;
Dt = 0.004; T = 0;
while (T <50) {
Q1=P1+Dt*(-A*P1+A*P2);
Q2=P2+Dt*(-P1*P3+B*P1-P2);
Q3=P3+Dt*(P1*P2-C*P3);
glib_putpixel(Q1,Q2);
T=T+Dt;
P1=Q1; P2=Q2; P3=Q3;
}
}
end$
画面に描き出される次のような不思議な軌道に感動していただきたい.
章末問題
- 減衰振動の方程式
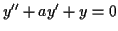 を数値的に解きなさい.
パラメータ
を数値的に解きなさい.
パラメータ 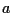 を変えるとどうなるか?
を変えるとどうなるか?
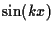 および
および 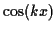 を組み合わせて面白いグラフを作ろう.
を組み合わせて面白いグラフを作ろう.
- Lorentz 方程式の解を, パラメータ, 初期値を変えて観察しよう.
- 連立常微分方程式の場合に差分法の解の収束証明をしなさい.
- 差分法の解の収束定理において, 誤差が
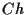 でなく
でなく
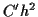 となるような差分スキームを考えなさい (2次のルンゲクッタ法).
となるような差分スキームを考えなさい (2次のルンゲクッタ法).
Nobuki Takayama
平成15年9月12日